מה זה ניתוח משוואות מבניות (SEM) וכיצד אפשר להשתמש בו בחינם?
הקדמה
מודל משוואות מבניות (SEM) הוא שיטה סטטיסטית חזקה שמשתמשים בה להערכת קשרים מורכבים בין משתנים. בניגוד לשיטות פשוטות יותר כמו ניתוח רגרסיה, SEM מאפשר לחוקרים לנתח קשרים ישירים ועקיפים (Direct + Indirect), מה שהופך אותו לכלי שימושי בתחומים כמו פסיכולוגיה, כלכלה ומדעי החברה.
בבסיסו, SEM משלב שתי טכניקות סטטיסטיות: ניתוח גורמים וניתוח נתיבים. שילוב ייחודי זה מאפשר לחוקרים להעריך כיצד משתנים נצפים (נתונים מדידים) קשורים למשתנים בלתי נצפים, הידועים כמשתנים חבויים (לטנטיים), שמייצגים מושגים מופשטים כמו אינטליגנציה, מוטיבציה או דיכאון.
לדוגמה, בפסיכולוגיה, חוקרים עשויים להשתמש ב-SEM כדי לחקור כיצד יכולות קוגניטיביות שונות (משתנים נצפים) תורמות למבנה בסיסי כמו אינטליגנציה (משתנה חבוי). SEM מספק דרך לבחון בו-זמנית מערכות יחסים מרובות, ומציע תובנות ששיטות מסורתיות מתעלמות מהן לעתים קרובות.
אחת מנקודות החוזק המרכזיות של SEM היא היכולת שלה לבדוק קשרים סיבתיים, לעזור לחוקרים לבדוק השערות לגבי הכיוון והחוזק של קשרים אלה. על ידי שילוב של משתנים נצפים ומשתנים חבויים, SEM מציע מסגרת מקיפה להבנת מבני נתונים מורכבים.
במדריך זה, נפרק את SEM לחלקים פשוטים, נחקור את מושגי המפתח שלו, יישומי העולם האמיתי ודוגמה שלב אחר שלב כדי לעזור לכם להתחיל עם SEM במחקר שלכם.
ניתוח נתיבים
ניתוח נתיב (Path Analysis) הוא הרחבה מיוחדת של ניתוח רגרסיה (Regression Analysis) המאפשרת לחוקרים לבחון את הקשרים הישירים והעקיפים בין משתנים. במודל רגרסיה סטנדרטי, אתם מוגבלים להערכת ההשפעה של משתנים בלתי תלויים על משתנה תלוי בודד. ניתוח נתיב מרחיב על כך על ידי מתן אפשרות לניתוח של משתנים תלויים מרובים וקשרי הגומלין ביניהם. זה בעצם ההמשך לניתוח שונות רב משתני (MANOVA), וניתוח מיתון ותיווך (Moderation & Mediation).
לדוגמה, שקול מודל שבו תמיכה משפחתית משפיעה הן על ההערכה העצמית והן על הביצועים הלימודיים. ניתוח נתיב מאפשר להעריך לא רק את ההשפעות הישירות של תמיכה משפחתית על כל תוצאה אלא גם את ההשפעות העקיפות (למשל, כיצד הערכה עצמית מתווך את הקשר בין תמיכה משפחתית לביצועים אקדמיים).
דיאגרמות נתיב משמשות בדרך כלל כדי להמחיש קשרים אלה. החצים מייצגים נתיבים סיבתיים בין משתנים, המאפשרים פרשנות קלה של מודלים מורכבים.
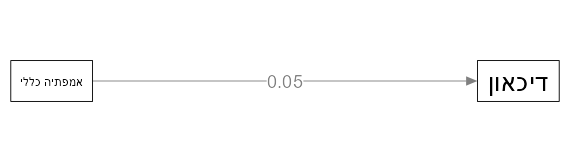
כאן לדוגמא יש נתיב שמסביר את ערכי הבטא (התרומה של המשתנה אמפתיה לשונות המוסברת R2 של המשתנה התלוי דיכאון). אמפתיה בעצמה לא מסבירה הרבה מהדיכאון. מה אם נוסיף עוד משתנה שמשפיע על דיכאון? למשל חרדה.
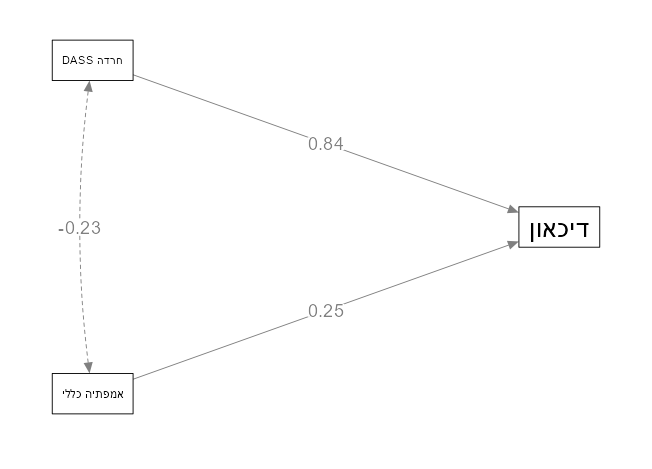
כאן, אנחנו רואים שהחרדה מסבירה הרבה מהדיכאון, והאמפתיה מסבירה טוב יותר את הדיכאון. ישנו קשר שלילי חלש בין אמפתיה לחרדה.
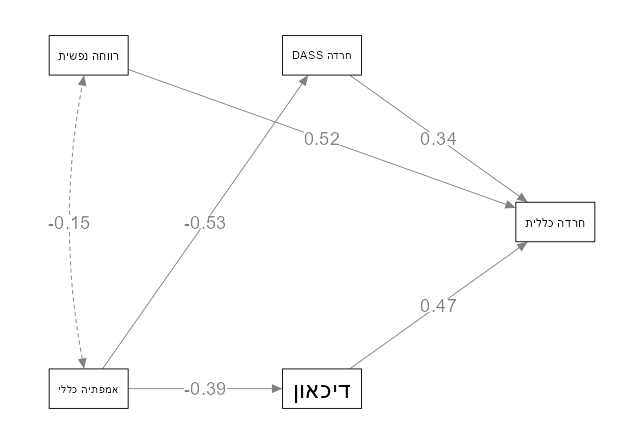
אפשר גם לבדוק מיתון ותיווך. פשוט מוסיפים קשר סיבתי בין המשתנים. למשל, כאשר החרדה מתווכת את הקשר בין אמפתיה לדיכאון.

כעת אנחנו מבינים שאמפתיה משפיעה על חרדה באופן שלילי, ואז החרדה משפיעה על הדיכאון באופן חיובי. בעצם אנחנו בונים מודל שאז אנחנו יכולים לבדוק אותו באמצעות נתונים. האם הוא מתאים לנתונים שלנו? האם התאוריה שבנינו מתאימה למציאות?
ניתוח נתיבים יכול להיות גם מאוד מורכב, ולכלול המון משתנים תלויים ובלתי תלויים, מתווכים וממתנים. אפשר גם כן, לבדוק הבדלים בין מודלים בהתאם למשתנים קטגוריאליים.
ניתוח גורמים
בעוד שניתוח נתיבים מתמקד במשתנים נצפים, ניתוח גורמים מציג את המושג של משתנים חבויים (לטנטיים) - מבנים תאורטיים לא נצפים המוסקים מנתונים הניתנים למדידה.
ניתוח גורמים משמש לצמצום מספר רב של משתנים לפחות גורמים בסיסיים, מפשט את מבנה הנתונים תוך שמירה על המידע החשוב ביותר.
לדוגמה, בפסיכולוגיה, חוקרים משתמשים לעתים קרובות בניתוח גורמים כדי לצמצם קבוצה גדולה של משתתפים שנמדדו אצלם מדדים בסיסיים כמו חרדה, דיכאון או רווחה. משתנים חבויים אלה מייצגים מושגים תיאורטיים שלא ניתן למדוד ישירות אך ניתן להסיק משאלות או התנהגויות קשורות.
ישנם שני סוגים עיקריים של ניתוח גורמים:
ניתוח גורמים גישושי (Exploratory Factor Analysis): משמש כאשר אין מבנה מוגדר מראש וברצונך לחקור כיצד משתנים שונים מתקבצים יחדיו.
ניתוח גורמים אישושי (Confirmatory Factor Analysis): משמש כאשר יש לך מודל מוגדר מראש, וברצונך לבדוק אם הנתונים שלך מתאימים למודל זה. המודל בעצם בודק עד כמה טוב הגורמים התאורטיים (החבויים) מסבירים את הנתונים (הפריטים עצמם במדגם מסוים).
בדרך כלל יש ערכי התאמת מודל (Model Fit) כמו ראמזי למשל (RMSEA) שמסבירים עד כמה המודל מתאים לנתונים. ערך ראמזי שהוא פחות מ-0.08 מעיד על מודל מותאם היטב.
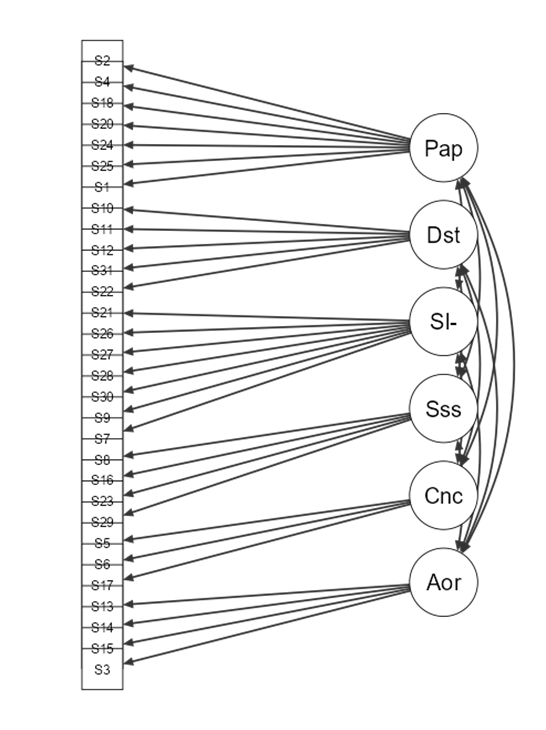
ניתוח משוואות מבניות (SEM)
SEM משלב את ה-CFA וניתוח הנתיב במסגרת כוללת אחת. הוא מאחד את מודל המדידה (CFA) ואת המודל המבני (ניתוח נתיבים), ומאפשר לחוקרים:
- למדוד משתנים חבויים באמצעות CFA, על ידי ניתוח עד כמה המדדים הנצפים משקפים משתנים תאורטיים.
- לבחון קשרים בין משתנים חבויים לנצפים בעזרת ניתוח נתיבים כדי להעריך קשרים סיבתיים או מתווכים.
לדוגמה, SEM יכול למפות כיצד משתנים חבויים כמו הערכה עצמית וחרדה (שנמדדו באמצעות CFA) משפיעים אחד על השני, וכיצד הם משפיעים על משתנים נצפים כמו ביצועים לימודיים (שנבדקו באמצעות ניתוח נתיבים).
CFA מוודא מדידה מהימנה של משתנים חבויים, בעוד שניתוח נתיבים ממפה את הקשרים בין המשתנים. השילוב של שניהם במסגרת SEM מספק כלי עוצמתי לבדיקת מודלים מורכבים הכוללים משתנים נצפים וחבויים.
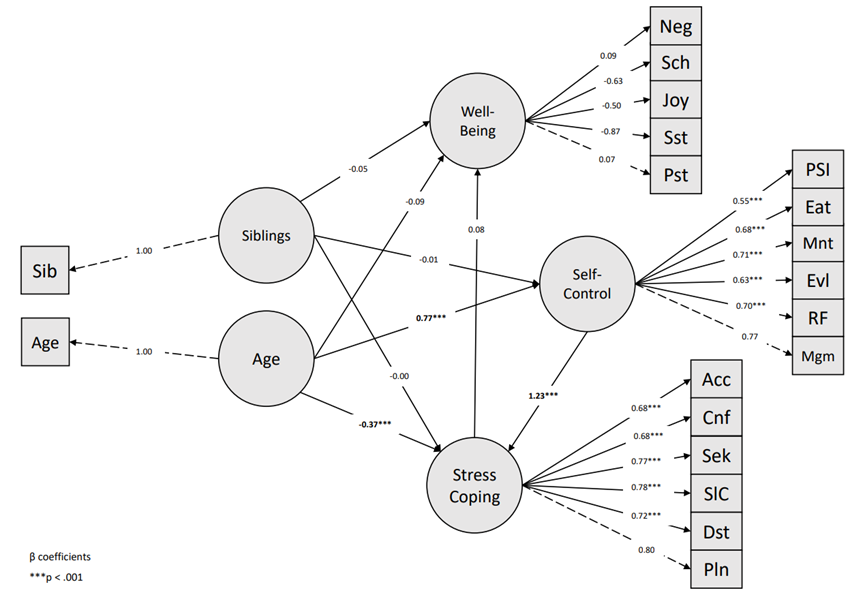
איך עושים ניתוח משוואות מבניות (SEM)
נכתוב כאן מדריך קצר למידול SEM בתוכנה R. יש תוכנות חינמיות כמו JASP, JAMOVI, R - שאפשר לעשות איתן ניתוח כזה.
אם אתם לא יודעים תכנות ב-R, לא נורא. יש לנו מדריך למתחילים ב-R.
אם יש לכם תאוריה שכוללת מבנים תיאורטיים תקפים (משתנים לטנטיים) עם קשרים סיבתיים ישירים ועקיפים באותו מודל, תנסו לצייר אותו על דף. תמתחו קווים בין המשתנים הלטנטיים כדי להסביר קשרים בין המשתנים. בנוסף, תמתכו קווים מכל הגורמים הלטנטיים שמסבירים את הנתונים שיש בידכם (הנתונים שמדדתם). זה יכול להראות כמו משהו כזה:
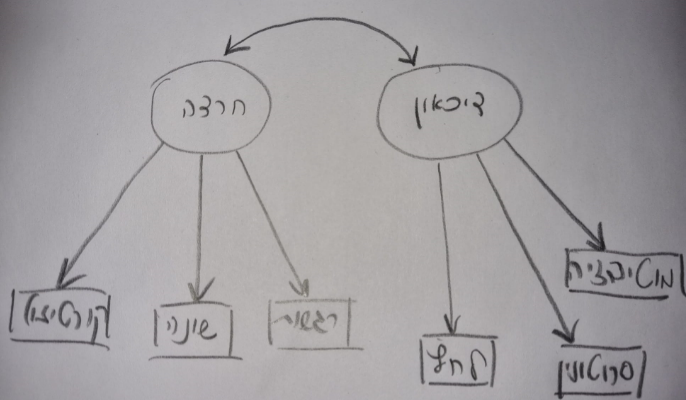
יש במודל 2 משתנים חבויים (חרדה ודיכאון). את החרדה והדיכאון מרכיבים אינדיקטורים (רגשות, שינה וקורטיזול שמוסברים על ידי חרדה, ולחץ, סרוטונין ומוטיבציה שמוסברים על ידי הדיכאון). עד לכאן, הכל הוא תאורטי - המודל הוא תאורטי ומומצא.
נשתמש בדוגמא של המודל הזה בשביל להסביר ולהדגים מה זה מודל SEM.
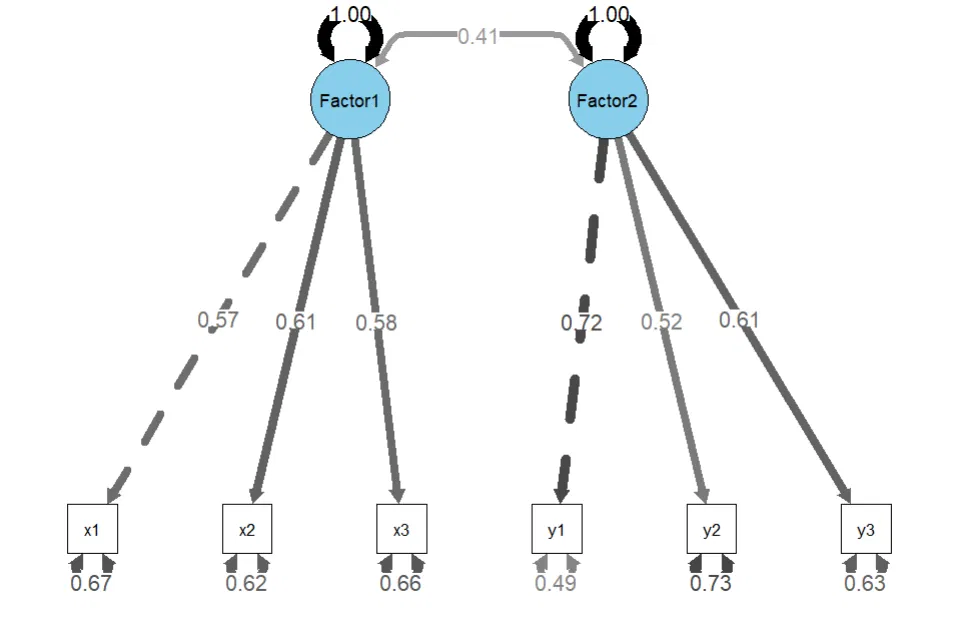
העיגולים הכחולים הם משתנים חבויים (או לטנטיים - Latent Variables). אלו משתנים תאורטיים, הם לא נמדדים באופן ישיר, אלא אנחנו מסיקים עליהם שהם קיימים דרך משתנים נצפים. הם נסתרים מהתפיסה שלנו ואפשר רק להסיק עליהם על סמך מדידות קיימות. הפריטים של כל משתנה חבוי זה בעצם מדידות שכן נצפו ושהן יכולות להסביר את המשתנה החבוי.
אז, להבדיל מניתוח גורמים, שבו אנו מנסים להסביר את הגורמים החבויים באמצעות הפריטים שאנחנו מודדים איתם (למשל, כמו לבדוק עד כמה שאלות על דיכאון מתקבצות לגורמים שונים שקשורים למשתנה לטנטי מסוים - דיכאון), בניתוח גורמים מאשש, או בגרסא היותר מורכבת שלו SEM, אנו מנסים להסביר את השונות בפריטים באמצעות המשתנים החבויים.
משתנים חבויים מאפשרים לחוקר לחקור על מבנים תאורטיים שיש קושי לצפות או למדוד אותם, אבל הם מאוד עוזרים להבין איך תופעה מסוימת מתרחשת. במילים אחרות, ככה חוקרים בעצם יכולים להבין איזה גורמם משפיעים על המשתנים הנצפים מאחורי הקלעים.
נניח שגורם 1 הוא חרדה, וגורם 2 הוא דיכאון.
הפריטים המרובעים הם משתנים שיכולים להסביר חלק מסוים מהגורם החבוי.
המספרים באמצעי החצים הם הטעינויות של המשתנים. הטעינות היא ערך שמסמל על היחס בין משתנה חבוי כמו מוטיבציה בלימודים למשתנה נצפה כמו השתתפות בשיעורים. זה קצת כמו מתאם. זה בעצם מראה עד כמה משתנה נצפה קשור למשתנה חבוי. או במילים אחרות, עד כמה שינוי במשתנה החבוי יביא לשינוי במשתנה הנצפה?
אנחנו יכולים לראות גם את הקשר בין 2 המשתנים החבויים, על סמך ששת המשתנים הנצפים. זה עוזר לנו להבין איך דיכאון וחרדה קשורים ונוטים להשתנות יחד.
החצים שנראים כמו חישוקים מסביב למשתנים הנצפים, זה השונויות של המשתנים. השונות של המשתנים הנצפים היא בעצם אחוז השונות שהיא מוסברת על ידי המשתנים החבויים. למשל, אם למשתנה שעות למידה יש שונות 0.67, זה אומר ש-67% מהשונות מיוחסת לשגיאות רעש או לגורמים אחרים שהם לא מוטיבציה בלימודים. משמע, ככל שהערך של השונות יותר קטן, זה אומר שהמשתנה מסביר טוב יותר את המשתנה החבוי ואינו מושפע מגורמים אחרים או הטיות. הסימון של השונות בעצם מסביר את מה שהמודל לא מסוגל להסביר, כולל טעויות מדידה, גורמים משפיעים אחרים או גורמים חבויים משפיעים נוספים.
המטרה הסופית במודלים של משוואות מבניות, היא להבין כיצד גורמים מרובים משפיעים אחד על השני. אפשר לבדוק ולבחון מבנים תאורטיים באמצעות משתנים חבויים. למשל אם אנחנו רוצים לבדוק שחרדה קשורה או משפיעה על דיכאון, אנחנו יכולים לבדוק את זה עם מודל כזה. בנוסף, אנו יכולים לכמת את ההשפעה של גורמים מתערבים, כמו גורמים מתווכים או ממתנים.
אפשרי להכין וליצור כל מני מודלים שמסבירים כל מני משתנים. תראו לדוגמא מודל SEM עם תיווך:
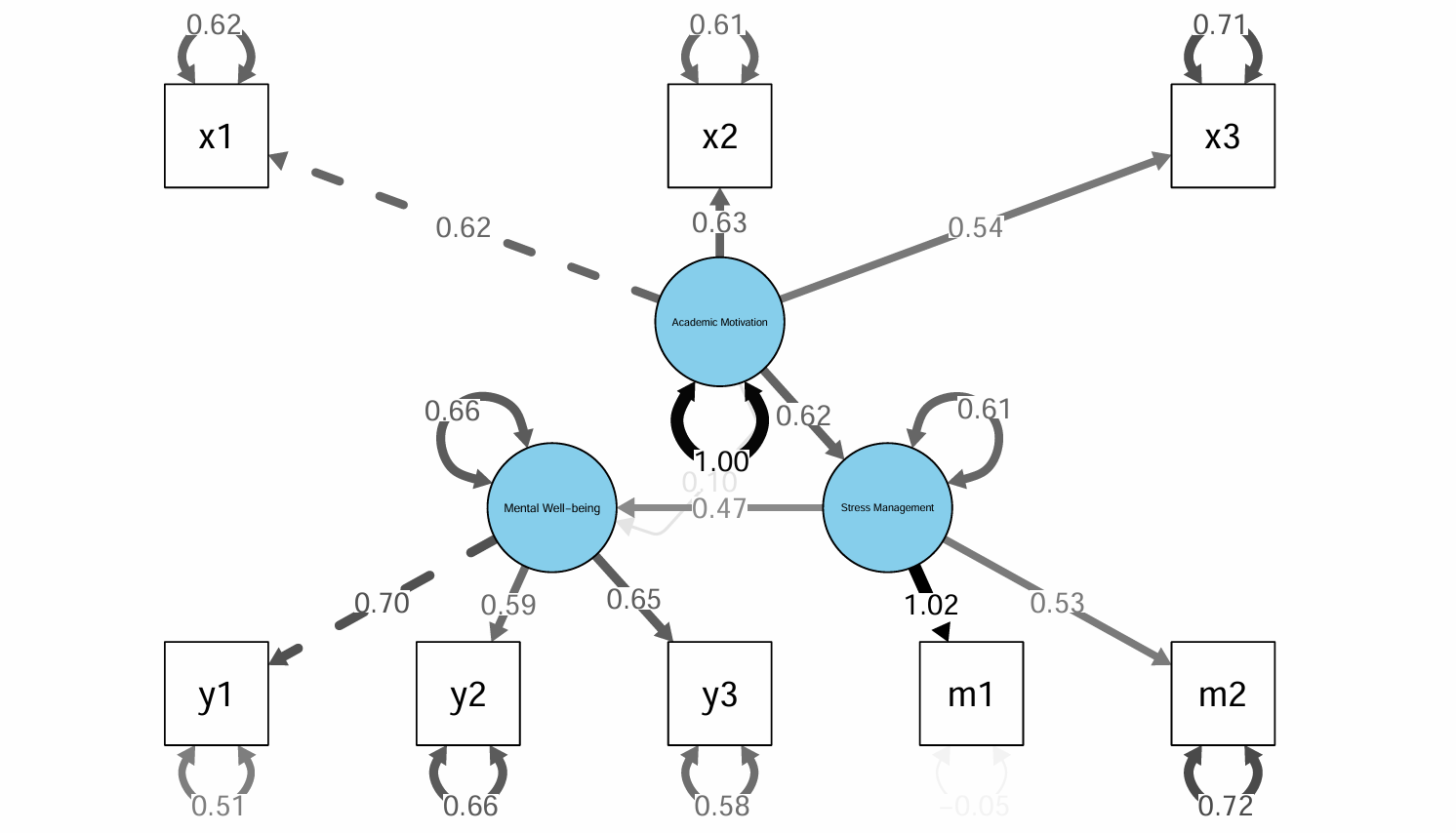
איך בונים מודל SEM ב-R
יש לנו מדריך למתחילים ב-R, בהקשר של סטטיסטיקה ופסיכולוגיה. אתם מוזמנים לעיין בו.
בואו נבנה מודל משוואות מבניות ב-R.
קודם כל נכנסים 2 חבילות חשובות לניתוח משוואות מבניות ב-R. אתם יכולים להעתיק את הקוד היישר לתוך תוכנת ה-R.
install.packages("lavaan")
install.packages("MASS")
library(lavaan)
library(MASS)נניח יש לנו גודל מדגם של 500 משתתפים. נוסיף מטריצה של המתאמים בין 2 משתנים חבויים (לטנטיים). אנחנו נעשה סימולציה לנתונים הללו, כך שהסימולציה תיצור לנו נתונים ל-2 משתנים חבויים על בסיס המתאמים ביניהם.
set.seed(42) n <- 500latent_cov <- matrix(c(1, 0.5, 0.5, 1), nrow = 2)latent_vars <- mvrnorm(n, mu = c(0, 0), Sigma = latent_cov)
כרגע יש לנו טבלה כזו, עם שני משתנים חבויים שיש ביניהם את המתאמים שהגדרנו (0.5, 1).
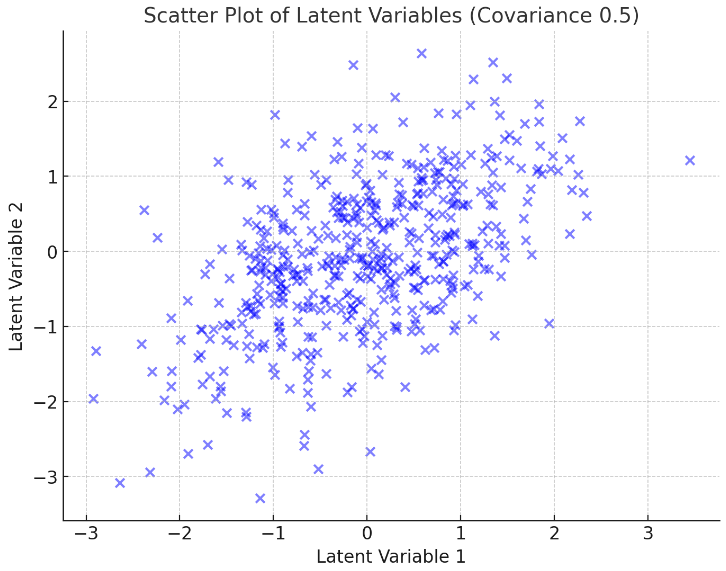
Y | X | |
-0.39163 | -0.76395 | 1 |
1.516016 | -0.17687 | 2 |
-0.28366 | 0.00856 | 3 |
-1.7604 | -0.9727 | 4 |
-0.61895 | 0.234427 | 5 |
... | ||
0.301655 | 0.975996 | 500 |
עכשיו נוסיף גם דרך סימולציה לכל משתנה, 3 פריטים כל אחד עם שונויות שונות. זה יהיה X1,X2,X3 וכו'.
x1 <- 0.7 * latent_vars[, 1] + rnorm(n, mean = 0, sd = 1) x2 <- 0.8 * latent_vars[, 1] + rnorm(n, mean = 0, sd = 1) x3 <- 0.6 * latent_vars[, 1] + rnorm(n, mean = 0, sd = 1) y1 <- 0.9 * latent_vars[, 2] + rnorm(n, mean = 0, sd = 1) y2 <- 0.7 * latent_vars[, 2] + rnorm(n, mean = 0, sd = 1) y3 <- 0.8 * latent_vars[, 2] + rnorm(n, mean = 0, sd = 1)
כרגע נשלב הכל במסגרת נתונים אחת:
simulated_data <- data.frame(x1, x2, x3, y1, y2, y3)
יצא לנו משהו כזה:
y3 | y2 | y1 | x3 | x2 | x1 | |
-0.99211 | -0.78574 | -1.17345 | -1.45417 | -1.21305 | -1.09524 | 1 |
1.787126 | 1.298149 | 1.057158 | -1.14608 | -1.13519 | -0.35399 | 2 |
-0.93144 | -0.74015 | -1.15739 | -0.01284 | 1.033633 | 1.5647 | 3 |
-1.94231 | -0.01306 | -0.9573 | -0.7158 | -0.0271 | -0.61038 | 4 |
0.279228 | -0.25913 | 0.563304 | -2.40869 | -1.32163 | 0.293387 | 5 |
עכשיו יש לנו טבלת נתונים שתתאים לניתוח SEM. בעצם יש לנו 3 משתנים של X ו-3 משתנים של Y. הקשרים בין המשתנים האלה מבוססים על ההנחה שיש קשר של 0.5 בין 2 המשתנים הלטנטים שהם מרכיבים (משתנה X ומשתנה Y). עכשיו, הצעד הבא הוא לבנות שלד של מודל, ללא נתונים. זהו מודל משוואות מבניות תאורטי.
סינטקס Lavaan
הגדרת משתנה לטנטי
=~
- סימון זה משמש להגדיר משתנה חבוי שמוסבר על ידי משתנים נצפים. לדוגמה, אם משתנה חבוי מיוצג על ידי מספר מדדים בשאלון, המשתנה החבוי "נמדד על ידי" המדדים הללו.
- דוגמה:
y =~ y1 + y2 + y3
כאן, המשתנה החבוי y נמדד על ידי המדדים הנצפים y1, y2, ו-y3.
רגרסיה
~
- סימון זה מציין קשר רגרסיבי, כלומר משתנה אחד נגרם או מושפע על ידי משתנה אחר.
- דוגמה:
m ~ y1
כאן, המשתנה הנצפה m מוסבר על ידי המשתנה החבוי y1
שונות (או קווריאציה)
~~
- זהו סימון לקשר של קווריאציה או שונות בין שני משתנים. לדוגמה, ניתן להגדיר שונות עבור משתנה בודד או קווריאציה בין שני משתנים שונים.
- דוגמה:
y1 ~~ y2
כאן, יש קשר של קווריאציה בין y1 ל-y2. - דוגמה לשונות:
y1 ~~ y1
זה מייצג את השונות של y1.
נוסחת חיתוך (intercept)
~ 1
- מציין את הנקודה שבה המשתנה חותך את הציר כאשר אין משתנים מסבירים. בדרך כלל, זה מגדיר את נקודת האפס של המשתנה.
- דוגמה:
y1 ~ 1
כאן, מוגדר החיתוך של y1.
באמצעות ארבעת סוגי הנוסחאות הללו, ניתן לתאר מגוון רחב של מודלים עבור משתנים חבויים.
- האופרטור
=~משמש להגדרת משתנים חבויים על ידי מדדים נצפים. - האופרטור
~מייצג קשרים רגרסיביים. - האופרטור
~~מייצג קווריאציה או שונות. - התחביר
~ 1מגדיר את החיתוך של המשתנה.
נמשיך עם הדוגמא הקודמת שלנו של בניית המודל ב-R.
sem_model <- ' Factor1 =~ x1 + x2 + x3 Factor2 =~ y1 + y2 + y3 Factor1 ~~ Factor2'
fit <- sem(sem_model, data = simulated_data) summary(fit, fit.measures = TRUE, standardized = TRUE)
install.packages("semPlot")library(semPlot)semPaths(fit, what = "std", layout = "tree", edge.label.cex = 1, curvePivot = TRUE, nCharNodes = 0, style = "ram", nodeLabels = c("x1", "x2", "x3", "y1", "y2", "y3", "Factor1", "Factor2"), edge.color = "black", color = list(lat = "skyblue", man = "white"), mar = c(5, 5, 5, 5))
אז נקבל לנו גרף נחמד כזה (של חבילת semPlots, עם הטעינויות של כל פריט לגורם שלו, והמתאם בין הגורמים.
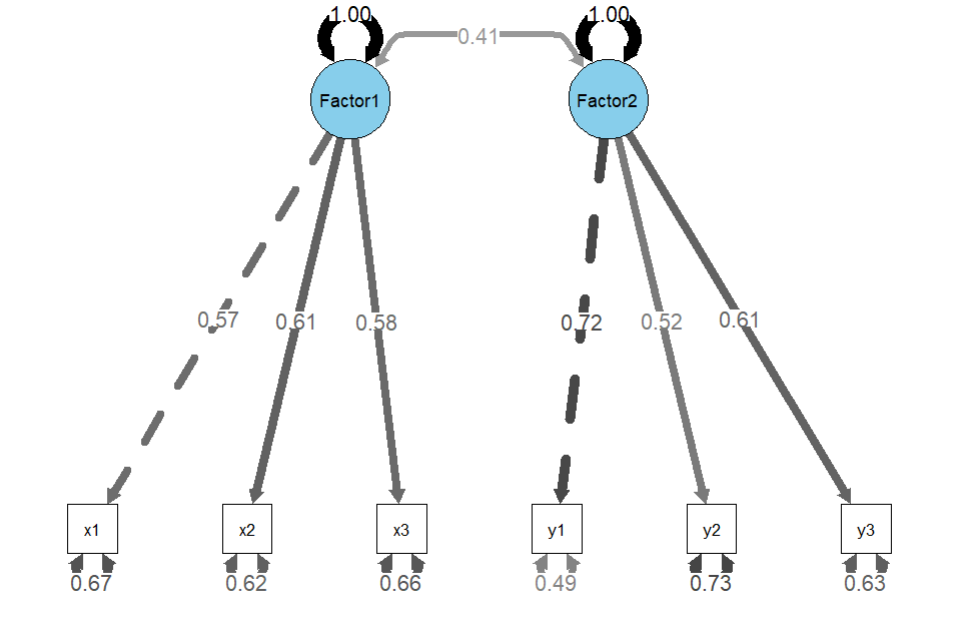
אפשר גם בסגנון מעגלי אם משנים את ה-Layout.
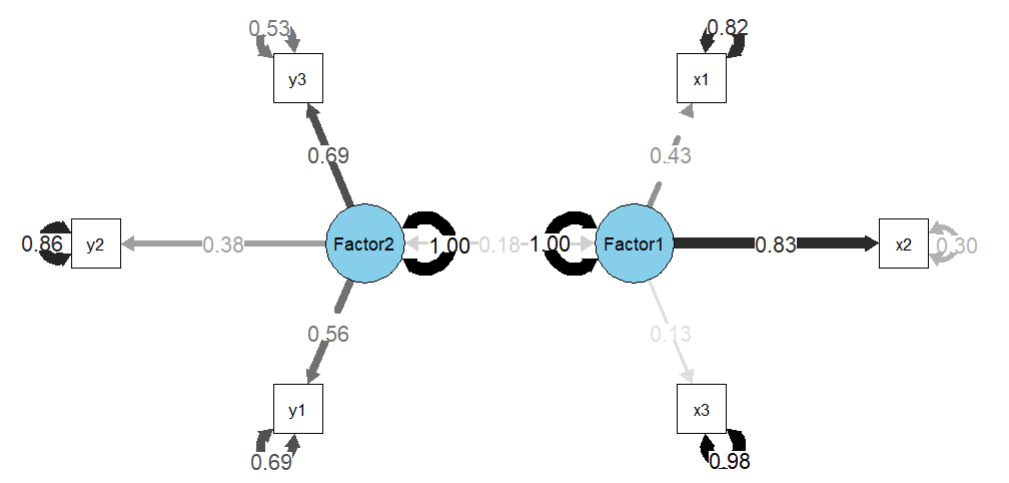
אפשר ליצור גרפים למודלים כאלו בחבילות אחרות כמו qgraph:
install.packages("qgraph")library(qgraph)fit <- sem(sem_model, data = simulated_data)std_solution <- standardizedSolution(fit)graph(std_solution[,c("lhs", "rhs", "est.std")], layout = "spring", vsize = 10, esize = 20, labels = c("x1", "x2", "x3", "y1", "y2", "y3", "Factor1", "Factor2"), edge.color = "blue")
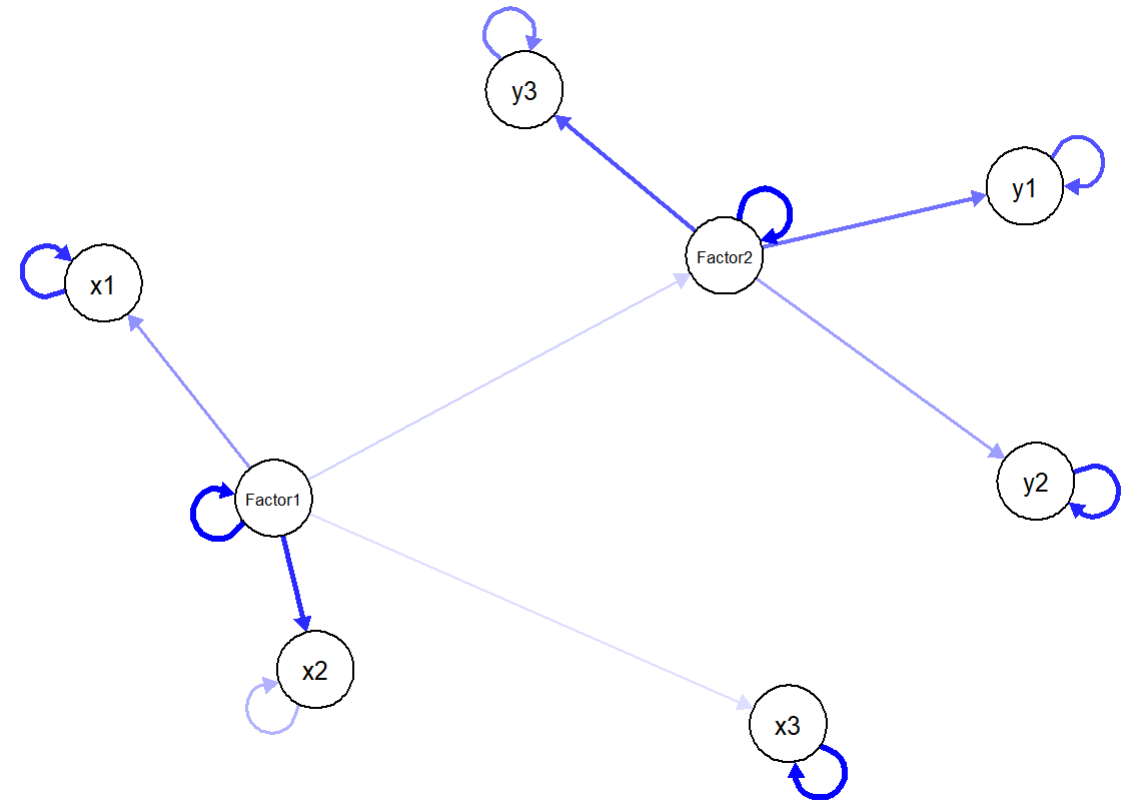
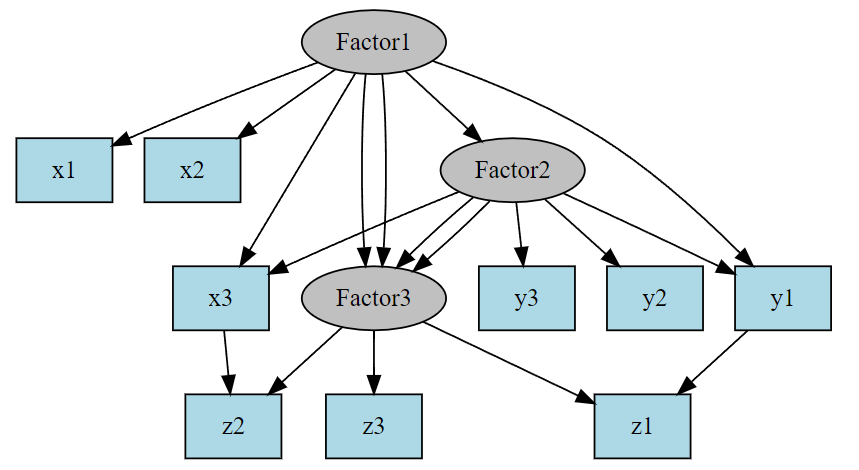
אפשר להשתמש גם בחבילות אחרות לבניית גרפים של SEM, כמו למשל החבילה "DiagrammeR".
הבנת זיהוי מודל (Model Justification)
ב-מודלים של משוואות מבניות (SEM), אחד ההיבטים הקריטיים ביותר הוא זיהוי המודל. כדי שמודל SEM יוכל להיות מוערך בהצלחה, הוא חייב להיות מזוהה, כלומר חייבים להיות מספיק נתונים כדי להעריך את כל הפרמטרים של המודל. בואו נפרק את המושגים המרכזיים הקשורים לזיהוי, התכנסות, פרמטרים, והדרישות לבניית מודל SEM טוב.
מהו זיהוי מודל?
זיהוי מודל מתייחס לשאלה האם ישנם מספיק נתונים זמינים כדי להעריך את הפרמטרים של המודל. הדבר נקבע על ידי השוואת מספר הידועים (מידע שקיים בנתונים) למספר הלא ידועים (פרמטרים שצריך להעריך במודל). קיימים שלושה סוגי זיהוי מודלים:
- מודל הוא מזוהה בדיוק (just-identified) כאשר מספר הידועים (נתונים) שווה בדיוק למספר הלא-ידועים (פרמטרים). במצב זה ניתן לפתור את המודל בצורה מושלמת, אך לא ניתן לבדוק כיצד המודל מתאים לנתונים מכיוון שאין דרגות חופש להערכת שגיאות.
- מודל הוא ביתר-זיהוי (over-identified) כאשר יש יותר ידועים מאשר לא-ידועים. זהו המצב הרצוי ב-SEM מכיוון שהוא מאפשר דרגות חופש – מקום לבדיקת התאמת המודל לנתונים. במודלים כאלה ניתן להעריך עד כמה המודל מתאים לנתונים על ידי בדיקת השאריות (ההבדלים בין תחזיות המודל לנתונים בפועל).
- מודל הוא בתת-זיהוי (under-identified) כאשר יש יותר לא-ידועים מאשר ידועים, כלומר אין מספיק מידע כדי להעריך את כל הפרמטרים. במודלים כאלה יש בעיה מכיוון שלא ניתן לפתור אותם, והתוכנה תחזיר שגיאה או תיכשל בהערכת הפרמטרים.
מהם פרמטרים ב-SEM?
ב-SEM, פרמטרים הם הכמויות הלא-ידועות שהמודל מעריך על בסיס הנתונים. הם יכולים לכלול:
- משקולות פקטורים (Factor loadings) – עד כמה כל משתנה נצפה קשור למשתנה חבוי,
- נתיבי רגרסיה – קשרים בין משתנים,
- שונויות וקווריאציות – עד כמה משתנים משתנים זה עם זה,
- חיתוכים וממוצעים – ערכים התחלתיים של משתנים.
המטרה של SEM היא להעריך פרמטרים אלה בצורה הטובה ביותר בהתבסס על הנתונים.
מהי התכנסות?
התכנסות מתרחשת כאשר האלגוריתם של SEM מוצא קבוצה של הערכות פרמטרים שמתאימות בצורה הטובה ביותר לנתונים על פי המודל שצויין. האלגוריתם מנסה להקטין את ההבדל בין תחזיות המודל לבין הנתונים בפועל (בדרך כלל באמצעות שיטות כמו הערכת סבירות מקסימלית - Maximum Likelihood).
- מודל שהתכנס: כאשר האלגוריתם מצליח למצוא הערכות לכל הפרמטרים, אומרים שהמודל התכנס (Converged).
- אי-התכנסות: אם האלגוריתם לא מצליח למצוא פתרון מתאים (למשל, בגלל תת-זיהוי או ערכי התחלה בעייתיים), המודל אינו מתכנס (Did not converge). אי-התכנסות יכולה להתרחש בגלל:
- יותר מדי פרמטרים חופשיים (לא-ידועים),
- גודל מדגם לא מספיק,
- הגדרת מודל שגויה (למשל, קשרים לא ריאליים בין משתנים),
- נתונים שאינם נורמליים.
התכנסות היא חיונית מכיוון שבלעדיה, הערכות המודל והתוצאות אינן אמינות.
מה צריך בשביל מודל SEM טוב
מספר המשתתפים או התצפיות הנדרשים עבור SEM הוא נושא שנחקר רבות, אך ישנם קווים מנחים כלליים שיעזרו להבטיח שהמודל יוכל להיות מוערך בצורה אמינה:
- חוקים כלליים:
כלל אצבע נפוץ הוא שצריך לפחות 5-10 משתתפים לכל פרמטר במודל. לדוגמה, אם המודל מעריך 20 פרמטרים, תצטרכו בין 100 ל-200 משתתפים. - המלצות לגודל מדגם:
- עבור מודלים פשוטים יותר: 100–200 משתתפים עשויים להספיק.
- עבור מודלים בינוניים: 200–400 משתתפים מומלצים בדרך כלל.
- עבור מודלים מורכבים: עדיף 400 משתתפים ומעלה, במיוחד אם יש הרבה משתנים חבויים או נתיבים.
- גודל מדגם מינימלי:
ישנם חוקרים הממליצים על 200 משתתפים כמינימום עבור רוב מודלי SEM, שכן זה מאפשר איזון בין יציבות הערכות הפרמטרים לבין מורכבות המודל.
עם זאת, גודל המדגם אינו רק פונקציה של מספר המשתתפים – גם איכות הנתונים והאופן שבו המודל מתאים למבנה התאורטי הם חשובים.
כיווני המשך
ישנם הרבה כיוונים להמשיך ללמוד ולהתקדם בתחום הזה של משוואות מבניות. אפשר לכתוב על הנושא הזה ספרים שלמים.
אם אתם סטודנטים או חוקרים שצריכים סיוע סטטיסטי בניתוח משוואות מבניות, אתם מוזמנים להשאיר הודעה.
אנחנו מתכננים להוציא קורס מקיף על ניתוח משוואות מבניות (SEM), המותאם למתחילים ולמתקדמים יחד.
הקורס יעניק לכם כלים לבנות ולנתח מודלים סטטיסטיים מורכבים, כולל ניתוח נתיבים, ניתוח גורמים, ומיתון ותיווך. למתחילים, נלמד את העקרונות הבסיסיים ונכיר את הכלים והתוכנות המרכזיות כמו R ו-Lavaan, בעוד שלמתקדמים נציע טכניקות ניתוח מתקדמות ותרגולים מעמיקים יותר עם נתונים אמיתיים.
הקורס יהיה פתוח בעתיד, בהתאם לביקוש ולהודעות שיתקבלו. אם אתם מעוניינים ורוצים שנודיע לכם כשהקורס יצא, השאירו פרטים ונעדכן בהקדם!
סיכום
מודל משוואות מבניות (SEM) הוא כלי עוצמתי המאפשר לחוקרים לחקור מערכות קשרים מורכבות בין משתנים, כולל משתנים חבויים שאינם נצפים ישירות. הוא מספק מסגרת ייחודית לשילוב ניתוח גורמים וניתוח נתיבים, מה שמאפשר לחוקרים לבחון השפעות ישירות ועקיפות בין משתנים. כדי להבטיח הצלחה בבניית מודל SEM, חשוב לוודא שהמודל מזוהה כראוי, שיש מספיק תצפיות לכל פרמטר, והמודל עצמו מתוכנן היטב בהתבסס על תאוריה מבוססת. שמירה על כללי אצבע כמו יחס של לפחות 5-10 תצפיות לכל פרמטר, וזיהוי ביתר של המודל יובילו להתכנסות טובה יותר של האלגוריתם ולקבלת תוצאות אמינות. ניתוח SEM הוא שיטה שימושית במיוחד בפסיכולוגיה, כלכלה, ומדעי החברה להבנת קשרים מורכבים בין משתנים.